Can COViD break Alice’s design?
This is the second challenge from the Cryptography section of Stack-The-Flag 2020 by govtech-csg. It uses LFSR stream cipher to encrypt 500 bytes of data and is an extended challenge from “Can COViD steal Bob’s idea?”.
Statement
We are given a txt file contains 500 bytes expressed in hexadecimal.
This is the image from the zip file in challenge 1.
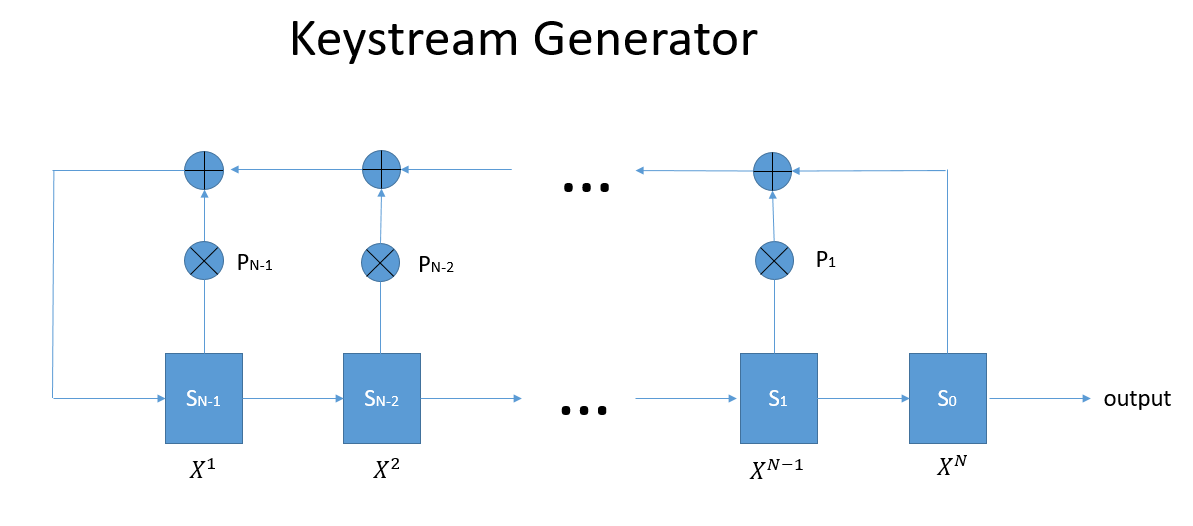
Also recall the statement given by Bob to Alice.
Hi Alice, could you please help me to design a keystream generator according to the file I share in the file server so that I can use it to encrypt my 500-bytes secret message? Please make sure it run with maximum period without repeating the keystream.
Observation
The first thing I tried to do is google about keystream generator. I found out about stream cipher and it uses a similar notation as the image.
However, I was still very confused about what the image means. Why are there \(X^{i}\) , \(P_{i}\) , \(S_{i}\) , \(\oplus\) and \(\otimes\) in the pictures. Also, why are the arrows pointing back to itself.
I stucked here for several hours and finally I found a youtube video lecture used the exact same notations as the image.
Thanks to the professor, I realized that the image is just linear-feedback shift register (LFSR).
Linear-feedback Shift Register
Introduction
The whole idea of LFSR is to use short bytes to generate one-time pad (OTP) for XOR encryption.
XOR with perfectly random OTP has been proven to be perfectly secured, but it is not practical when we have to encrypt long bytes. Usually in XOR encryption, the key gets repeated when the message has a longer bytes than the key. The repetition of key makes it vulnerable to frequency analysis.
Therefore, LFSR is developed to fix this issue. We give the system some random initial value and the size of the message we want to encrypt. LFSR will generate out a OTP for us to do the encryption.
Technical details
How does LFSR generate the OTP?
Let’s say you have \(N\) shift register in a LFSR. So that gives you \(S_{0},S_{1},S_{2},\cdots,S_{N-1}\).
This means that the initial value should also has \(N\) bytes to put in every register.
The OTP will start with these initial value.
Then, the system generate the next bytes with the following equation
let \(P_{i} \in \{0,1\}\)
\[S_{N+i} = (P_{0}\cdot S_{i} + P_{1}\cdot S_{i+1} + \cdots + P_{N-1+i}\cdot S_{N-1+i})\ \underline{mod}\ 2\]That is,
\[S_{N} = (P_{0}\cdot S_{0} + P_{1}\cdot S_{1} + \cdots + P_{N-1}\cdot S_{N-1})\ \underline{mod}\ 2\] \[S_{N+1} = (P_{0}\cdot S_{1} + P_{1}\cdot S_{2} + \cdots + P_{N-1}\cdot S_{N})\ \underline{mod}\ 2\] \[S_{N+2} = (P_{0}\cdot S_{2} + P_{1}\cdot S_{3} + \cdots + P_{N-1}\cdot S_{N})\ \underline{mod}\ 2\] \[\vdots\]Looking back at the diagram, The \(\otimes\) means multiplication between \(S_{i}\) and \(P_{i}\). It is then send to \(\oplus\) which is essentially just addition with other values.
Every \(N+i\) byte will depends on the previous \(N\) bytes with some equation.
The reason people uses this to generate OTP is because the OTP generated looks random and has a very long cycle. A LFSR system with \(N\) shift register can has a maximum cycle length of \(2^{N}-1\).
Hence, if we wanted to encrypt a 1000 bytes message, we can just use a LFSR system with 10 shift register to generate the OTP. The generation process is also very fast as it is done in registry level.
Attempt
After understanding how LFSR works, this question should be easy now right … ?
Looking back at the text sent,
I can use it to encrypt my 500-bytes secret message? Please make sure it run with maximum period without repeating the keystream.
Bob did explicitly mention to let it run with maximum period. As the message is 500-bytes long, so means it needs a 4000 bits long OTP. Therefore we know there must be at least 12 shift registers in the system.
After doing some research, I found out that only primorial polynomial in Galious field of 2 will gives maximum period. I then try all the primorial polynomial and brute force the inital value.
Another thing I did was brute forcing all the possible starting from 12 shift register \(P^{i}\) and \(S^{i}\) and check if the decrypted text has govtech-csg{ flag format in it.
Unfortunately, since the runtime is approximately \(O(2^n)\), It got stuck shortly after and I couldn’t find anything interesting.
Solution
After failing and stuck for several hours again, I have a sudden realization that govtech-csg{ is actually quite long in terms of bits (it contains 96 bits). Also in practice, we usually dont use LFSR with too much shift registers. This gives me an idea on how to solve this question using the flag prefix.
Recall that
\[S_{N+i} = (P_{0}\cdot S_{i} + P_{1}\cdot S_{i+1} + \cdots + P_{N-1+i}\cdot S_{N-1+i})\ \underline{mod}\ 2\]Since there are 96 bits in govtech-csg{, I can form a linear system that consists of \(96-N\) equations, where \(N\) is the number of shift registers.
Then I solve the linear system and it will contain a solution for \(P_{0},P_{1},\cdots,P_{N-i}\) if it is consistent.
I also check if govtech-csg{ starts at somewhere in the middle of the secret message. Turns out it is!
Here’s the python code for the complete solution.
from Crypto.Util.number import long_to_bytes
from sage.all import * # this is mandatory to initialize Sage
m = "1CC4D4D98FA4E8BEC8269DA66A7DFACF946BFDDCFDFFC2530D28F79A00CDB3E94A65BEB4698B355863D1AA24F4CA1E9F9170A384DA7FD89E5F71DD7F015E8B7578B2B21A8873737821280D4553638EA36598261D4254710BD9C3876A9BCA9381FA78E9AE594405C32C5AC290B5BB717E9ECCAF7EDC4F75209AE0399E517D76A50B5A676C9D078836F9F4D351DB4208CB5EF35CD44240E197074239CB4F72126271178EAB3A964AEE7DB0C46BF3F16D154A85E4E44DE0F31DAEA0F8301DBE4686F3D31912E465ED6602DF37D3F5DC92B5A423206282489C6ADE9A4223BE5D722177491073AEB3497D284E2F2546189A42DA0BF5C1FF4462122AF88E016B78CDAE968DF2683515509C4BC63833CC2E18F9C9727E30BF3D55597EFD021FA4E39ED5201EA170986704B1ED9A61CCBCBDD7E4A08F78C7D4471DE8C1502BF6799E943F15D8E536E6DEA001549066F66020DD2C8A3615846E5DDD089BA776010A8B4A0E10DEC76E30888560EB1D5CE400880F15BFDE792570739CC897473DC86E6AEF90A1C806D7BEEF5F1E9768022FE8EED9971E99888951687BD90A46F5A52A3C08A3D46873B69551084C50D301FE89ED96EAD7D69B15BBAECDA1E143B63B791A081D3AB30DF46F8F7A5E64C38424272D1F671BA6A23601FC1A41A732F6379F5C70F369CC8BB95CD82CDE0AF9F7355E719B3A578ACF1A"
flag = "govtech-csg{"
R = IntegerModRing(2)
for s in range(0,len(m),2):
prefix = ""
# s is where the flag prefix starts
tm = m[s:]
# Convert the flag to bits and store it in prefix variable
for i in range(len(flag)):
t = m[s+i*2]+m[s+i*2+1]
temp = int(t,16)
prefix = prefix + format(ord(flag[i]) ^ temp,'08b')
for deg in range(12,int(len(prefix)/2)-1):
# deg here means number of shift register in the system
# Construct the linear system
A = []
b = []
for i in range(len(prefix)-deg):
A.append(list(map(int,prefix[i:i+deg])))
b.append(int(prefix[i+deg]))
M = Matrix(R, A)
b = vector(R, b)
try:
# solve the linear system
sol = M.solve_right(b)
otp = list(map(int,prefix))
# This whole part is to generate OTP using sol
while (len(otp) < len(tm)*8):
new = 0
for i in range(len(sol)):
new += otp[-len(sol)+i]*sol[i]
otp.append(new%2)
count = 0
# This whole part is just XOR cipher
for j in range(s,len(m),2):
h1 = int(m[j] + m[j+1],16)
h2 = int("".join(list(map(str,otp[count*8:(count+1)*8]))),2)
count += 1
print(str(long_to_bytes(h1^h2))[2:-1],end='')
print()
print()
except:
# If the linear system is not consistent
continue
I used sage to solve the linear system.
You can run this code using the following command
sage -python sol.py
flag : govtech-csg{Thi$_Lf$r_1s_N0t_$3cur3_5b26ac11c74fb63b}